ToME: the Tales of Maj'Eyal

Posted: **Thu Mar 03, 2011 9:17 pm**

I saw that the topic of how armor should work came up in IRC, and I want to chime in and let others discuss it here.

I'm in the camp that armor should "Just Work"(tm) and be smooth, as opposed to, say, having a flat reduction of damage and then applying a percentage of damage. It's sufficient to say what armor does in the description and not necessarily how it does it (and there may eventually be a well-written guide to explain such things

).

Anyway, here are various ways the damage is reduced (by %) from armor (contours every 10%):

Previously, "max(damage-armor, 0)" (I think)

: armor_previous.png (64.25 KiB) Viewed 6377 times

Currently, "damage*0.99^armor"

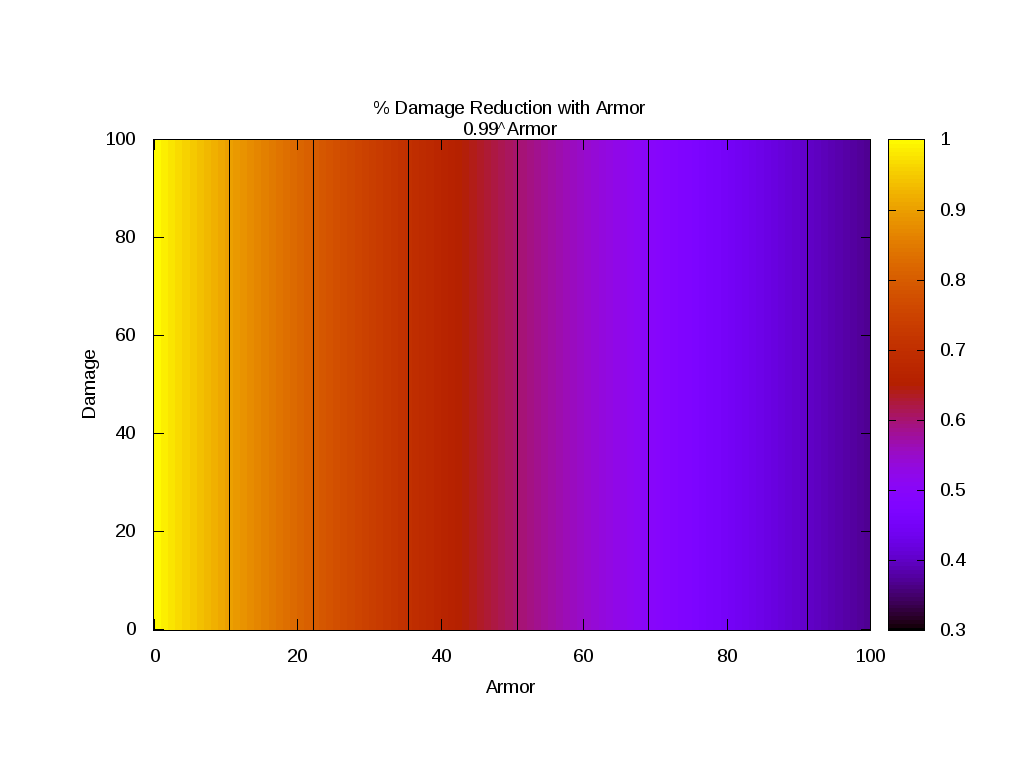
: armor_current.png (21.69 KiB) Viewed 6377 times

And I propose something of the form "damage*(0.99 - 0.01*armor/damage)^armor" (with damage > 0)

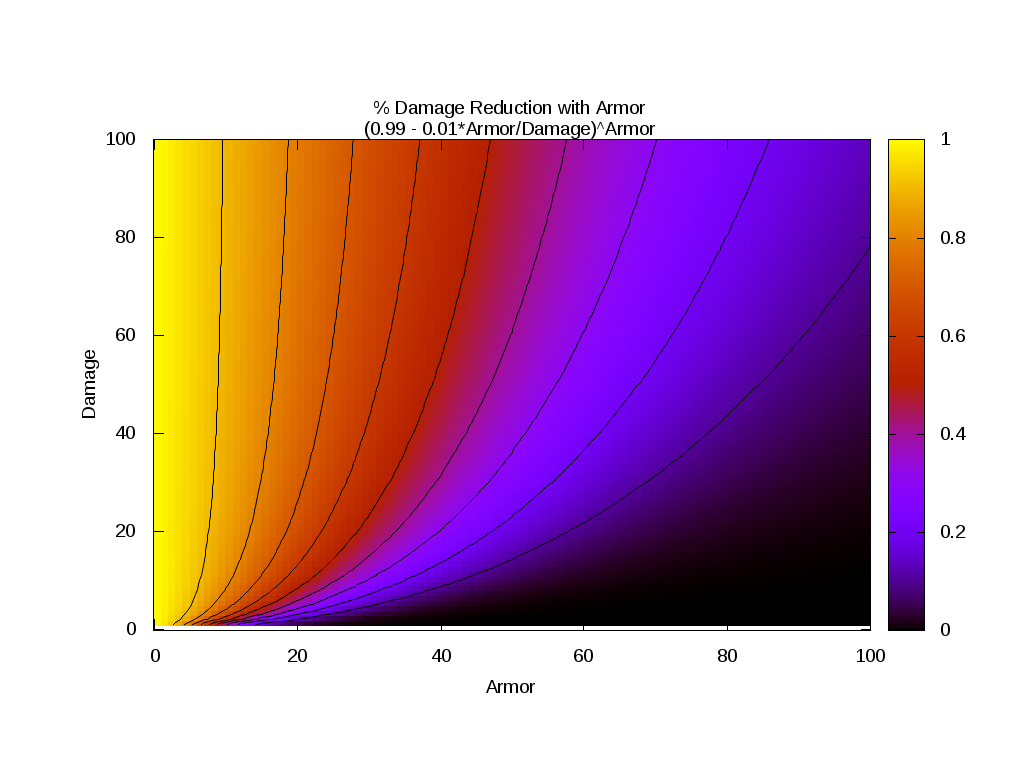
: armor_proposed1.png (62.12 KiB) Viewed 6377 times

As you can see, my proposed method is between the previous method and the current method, and it may be tweaked to give basically whatever behavior you want while still being smooth.

Posted: **Thu Mar 03, 2011 9:19 pm**

WOW those plots are large! My bad. If you want to mess around with the plots, here's how I made them in gnuplot:

Code: Select all

set pm3d at b
set palette
unset surface
set samples 101
set isosamples 101
set pm3d map
set contour
set cntrparam levels incremental 0.1,0.1,0.9
unset clabel
max(x,y) = (x>y)?x:y
set xlabel "Armor"
set ylabel "Damage"
set terminal png size 1024,768 large noenhanced truecolor

set output "armor_proposed1.png"
set title "% Damage Reduction with Armor\n(0.99 - 0.01*Armor/Damage)^Armor"
splot [0:100][0:100] (0.99-0.01*x/y)**x t "" w l lc -1

set output "armor_proposed2.png"
set title "% Damage Reduction with Armor\n(1.0 - 0.01*Armor/Damage)^Armor"
splot [0:100][0:100] (1.0-0.01*x/y)**x t "" w l lc -1

set output "armor_current.png"
set title "% Damage Reduction with Armor\n0.99^Armor"
splot [0:100][0:100] 0.99**x t "" w l lc -1

set output "armor_previous.png"
set title "% Damage Reduction with Armor\nmax(Damage-Armor, 0)/Damage"
splot [0:100][0:100] max(y-x,0)/y t "" w l lc -1

Posted: **Thu Mar 03, 2011 10:18 pm**

I would be in favour of this... Trying a armor heavy class (fighters) would show how easy/difficult the game becomes. My personal feeling is that the early game is pretty hard. :-/

Posted: **Thu Mar 03, 2011 11:34 pm**

Playing a wyrmic the armor change was pretty noticable early on in both directions. I was no longer Mr. Invincible but then again neither where the stone strolls when I was level 1.

I like the current armor system. I think it scales decently with incoming damage if not with every point of armor you gain.

The third method may be better though. I'm not sure and I've been on the computer to long to be bothered with trying to understand the formula right now.

Posted: **Fri Mar 04, 2011 12:27 am**

Yeah, I had a character that was maxing out armor (as well as abilities that do damage when hit

) instead of defense, and he was taking way more damage than I would have expected. If a character has armor of 100, why should an attack power of 9 still do 3 damage?! It makes no sense!

Anyway, I think I have a new method that is truly the best compromise between the previous method and the current method. I will detail the new method in the next message, because I need to show some plots first.

If we look at relative damage (i.e., damage/armor) versus armor, we can see just how different the previous and current methods are. Here they are:

Previous method:

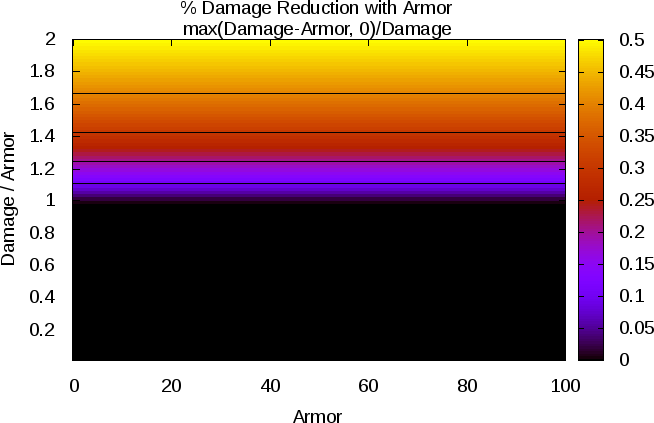
: armor_previous-relative.png (23.22 KiB) Viewed 6334 times

Current method:

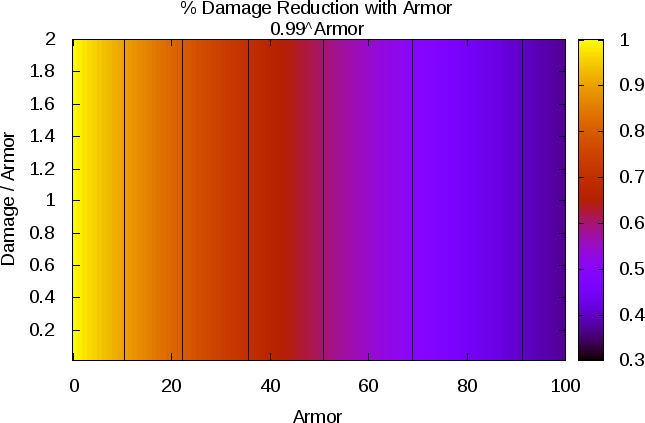
: armor_current-relative.png (19.74 KiB) Viewed 6334 times

And the method I proposed in the first post:

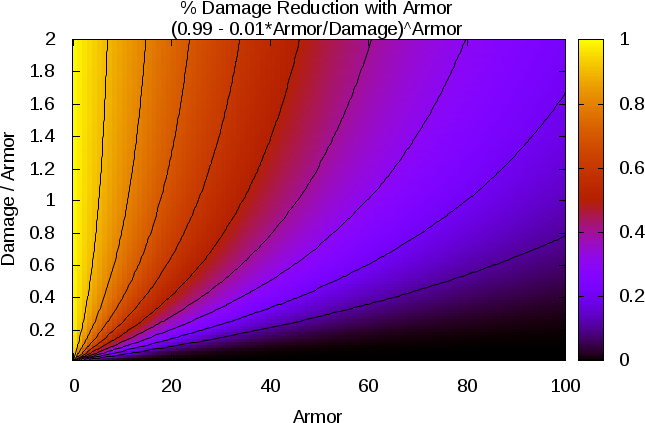
: armor_proposed1-relative.png (48.24 KiB) Viewed 6334 times

Posted: **Fri Mar 04, 2011 12:39 am**

Here's the same plot for my newest proposed method

alpha = 0.04 (explained later):

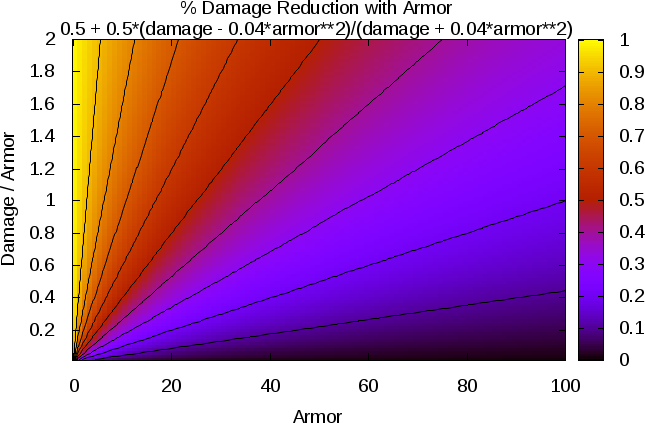
: armor_new-relative-alpha=0.4.png (50.09 KiB) Viewed 6330 times

alpha = 0.02:

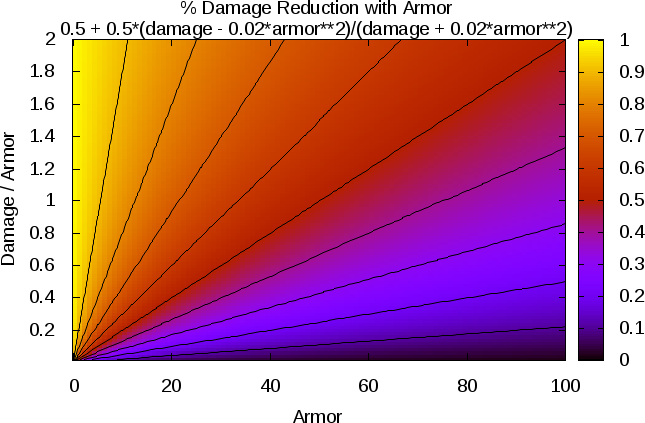
: armor_new-relative-alpha=0.2.png (48.98 KiB) Viewed 6330 times

If you compare these plots with the similar plots above, it should be obvious why I chose this method, which I will describe now:

Code: Select all

Final Damage = damage*(0.5 + 0.5*(damage - alpha*armor^2)/(damage + alpha*armor^2))

and the parameter "alpha" has an intuitive definition:

Code: Select all

                                       [(damage/armor) at 50% final damage]
alpha = [slope at 50% final damage] = --------------------------------------
                                           [armor at 50% final damage]

alpha = 0.04 seems reasonable, and here is a plot that shows the % damage taken vs armor, like the plots in the very first post:

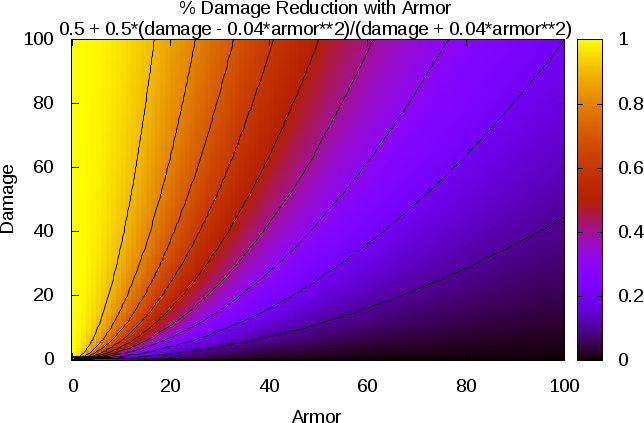
: armor_new-alpha=0.4.png (46.7 KiB) Viewed 6330 times

Thoughts?

Posted: **Fri Mar 04, 2011 1:03 am**

tiger_eye wrote:Thoughts?

You mean decides "ooo, plots"?

I like the latest method you suggested. The formula is complicated to explain, but I think the behavior will be quite intuitive. Basically we just tell people that high armor will completely block low amounts of damage (probably should add a cutoff so that we don't see a bunch of zeros floating up... or maybe that is good), and that as damage increases the effective reduction decreases.

Posted: **Fri Mar 04, 2011 2:22 am**

Your last suggestion definitely have a non-intuitive formula. First, the damage is compared to the square of the armor. Second, there is a point (damage = alpha*armor^2) where damage will be stuck to zero.

Personally, there are 3 features I like in my damage formulas:
1- Doubling both the attack and the defense double the resulting damage
2- Zero defense makes sense (ie: avoid things like damage = attack / defense)
3- It is impossible to reach zero average damage.

Obviously, all three of them are personal tastes more than anything else. But they guided my decision to use the following method for BOB:
For an attack of XdY and an armor of Z, the damage is:
D = \sum_{i=1}^X max[0, rnd(0,Y) - rnd(0,Z)]
Where rnd(0,A) is a random integer between 0 and A.

It works quite well, although its variance is quite large. Sadly, I don't think it would fit ToME, mainly due the way damage must in the form XdY...

Posted: **Fri Mar 04, 2011 2:49 am**

Alright, a discussion!

Marcotte wrote:Your last suggestion definitely have a non-intuitive formula.

Some of us don't think so

. Oh, and your formula isn't non-intuitive? (sorry, sorry, but we're allowed to reply to fallacious arguments with other fallacious arguments, aren't we?)

Marcotte wrote:First, the damage is compared to the square of the armor.

Don't forget the units of alpha! You're a fellow physicist, you should know better

. Also, I clearly showed the justifications and behavior of my method above. And isn't that what we're after? A function that behaves the way we want?

Marcotte wrote:Second, there is a point (damage = alpha*armor^2) where damage will be stuck to zero.

Not quite. You missed an additive factor of +0.5. Hence, "damage = alpha*armor^2" defines the locus where the final damage dealt is half the input damage. Which is reasonable behavior. And is also clear from the plots and equation.

I hope that clarified any confusion others may have had. Any other thoughts or questions?

Posted: **Fri Mar 04, 2011 3:07 am**

Marcotte wrote:Your last suggestion definitely have a non-intuitive formula.

I guess I shouldn't be so crass. Your criticism warrants that I should better describe the formula, especially since others are not as well technically trained as we are.

Let's construct a somewhat generic function based on the following behavior with inputs "damage" and "armor":

(1) if armor = 0, do 100% damage
(2) if damage >> armor, do 100% damage
(3) if armor >> damage, do 0% damage

Okay. This is somewhere to start. A simple generic function that exhibits this behavior is:

Code: Select all

f(damage, attack) = damage * ( 0.5  +  (FUNCTION1(damage) - FUNCTION2(armor)) / (FUNCTION1(damage) + FUNCTION2(armor)) )

where we choose FUNCTION1(x) and FUNCTION2(x) to be greater than or equal to 0 for all x.

We are free to choose FUNCTION1 and FUNCTION2, and the formula will satisfy our desired criteria. More generically:

Code: Select all

f(damage, attack) = damage * ( 0.5  +  (F1(damage)*G1(armor) - F2(damage)*G2(armor)) / (F1(damage)*G1(armor) + F2(damage)*G2(armor)) )

and so on. And, hey, perhaps we could choose better F1, F2, G1, and G2 to get the behavior we want, but this should at least dispel the notion that this formula is "non-intuitive".

Posted: **Fri Mar 04, 2011 3:14 am**

Note: in my post, I use "attack" as the generic variable which decides damage on the attacker side, and "defense" as the same but for the defender side. Sorry about that.

tiger_eye wrote:Alright, a discussion!
Marcotte wrote:Your last suggestion definitely have a non-intuitive formula.
Some of us don't think so . Oh, and your formula isn't non-intuitive? (sorry, sorry, but we're allowed to reply to fallacious arguments with other fallacious arguments, aren't we?)

Actually, I find my formula easier to understand (roll a die for the attack, roll one for the defense, damage is the difference, but cannot be lower than 0). Although if you want to see what the average damage is, it will be more complex than yours (there is a discontinuity at attack=defense).

tiger_eye wrote: And isn't that what we're after? A function that behaves the way we want?

You are right that should be the nearly exclusive concern, with intuitiveness as a minor concern.
Well, going by my three preferences:
1- Doubling attack and defense leads to less than double the damage. Quadrupling attack and double defense leads to quadruple the damage. That means that attack and defense are not on the same scale. This assume that if health increases linearly (as it does in ToME), then attack must also increase linearly (it is more than linear in ToME) and defense must increase as the square root (hard to say in ToME).
2- Zero defense makes sense: damage = attack in that case.
3- It is impossible to reach zero average damage (except for zero attack or infinite defense).

So two out of three, not bad, but can we find better?

tiger_eye wrote:
Marcotte wrote:Second, there is a point (damage = alpha*armor^2) where damage will be stuck to zero.
Not quite. You missed an additive factor of +0.5. Hence, "damage = alpha*armor^2" defines the locus where the final damage dealt is half the input damage. Which is reasonable behavior. And is also clear from the plots and equation.

My bad here. Now that I check again, you also only reach zero damage only at infinite armor.

Posted: **Fri Mar 04, 2011 3:26 am**

tiger_eye wrote:Let's construct a somewhat generic function based on the following behavior with inputs "damage" and "armor":

(1) if armor = 0, do 100% damage
(2) if damage >> armor, do 100% damage
(3) if armor >> damage, do 0% damage

Okay. This is somewhere to start.

I totally agree with this limit behaviors. My comment about intuitiveness is about the cases where you do intermediate damage (from 25% to 75%). That is what I don't really find intuitive about your formula, especially with the alpha parameter. I guess that the 50% point being at damage = alpha*armor*armor is not that hard to understand, but the comparison of a linear quantity with a squared quantity is what I called unintuitive. Although the power of weapons is already squared-rooted in the damage formula, which doesn't help matters...

So I would advocate a much simpler formula, for example:

Code: Select all

real damage = damage * (damage) / (damage + armor) = damage / (1 + armor/damage)

Then the 50% point is simply at damage = armor. And at armor >> damage, real damage is approximatively damage*damage/armor. And at armor << damage, real damage is approximatively damage - armor.
(BTW: the formula I use in BOB have the about the same limiting behavior, except that it is the 33% point which is at damage = armor.)

Posted: **Fri Mar 04, 2011 3:36 am**

I think we're nearing convergence, Marcotte

Doubling attack and defense leads to less than double the damage.

Quadrupling attack and double defense leads to quadruple the damage

I'm afraid I don't follow. How can both of these be true? Can you try explaining again?

So two out of three, not bad

Which one is it missing? In my newest method, doubling attack (input damage) and doubling the armor does lead to less than doubling of final damage.

And I agree, there is something nice about your method, but I don't think it's quite appropriate for ToME. btw, how large is X, Y, and Z typically?

but can we find better?

Back to my framework: I guess the salient question, then, is what locus for 50% final damage makes sense? The locus is defined as f(armor) = g(damage), or f2(armor, damage) = g2(armor, damage).

Posted: **Fri Mar 04, 2011 3:45 am**

tiger_eye wrote:I think we're nearing convergence, Marcotte
Doubling attack and defense leads to less than double the damage.
Quadrupling attack and double defense leads to quadruple the damage
I'm afraid I don't follow. How can both of these be true? Can you try explaining again?

Let assume a damage function d(X,Y), where X is the damage, Y is the armor, and d(X,Y) the real damage, after armor has been applied.
Then, with your suggestion:
d(2X,2Y) < 2 d(X,Y)
d(4X,2Y) = 4 d(X,Y)

tiger_eye wrote:
So two out of three, not bad
Which one is it missing? In my newest method, doubling attack (input damage) and doubling the armor does lead to less than doubling of final damage.

That's the one which is missing, I prefer to have damage functions such that d(2X,2Y) = 2 d(X,Y). But that's only a personal preference.

tiger_eye wrote: And I agree, there is something nice about your method, but I don't think it's quite appropriate for ToME. btw, how large is X, Y, and Z typically?

In BOB, health depends quadratically with the level, which is quite different to the situation in ToME. That said, I have X linearly increasing with level (but slowly), and both Y and Z also linearly increasing with level (but faster). So Y and Z stay in the same order of magnitude, while X counterbalance the quadratic increase in health. Obviously this won't work for ToME.

Posted: **Fri Mar 04, 2011 4:02 am**

Marcotte wrote:Let assume a damage function d(X,Y), where X is the damage, Y is the armor, and d(X,Y) the real damage, after armor has been applied.
Then, with your suggestion:
d(2X,2Y) < 2 d(X,Y)
d(4X,2Y) = 4 d(X,Y)

Oh, yes, this is true. And why is it bad? This method is squarely between the previous method and current method used in ToME, which was exactly the goal.

Below are relative damage plots using your suggestion

Marcotte wrote:real damage = damage * (damage) / (damage + armor) = damage / (1 + armor/damage)

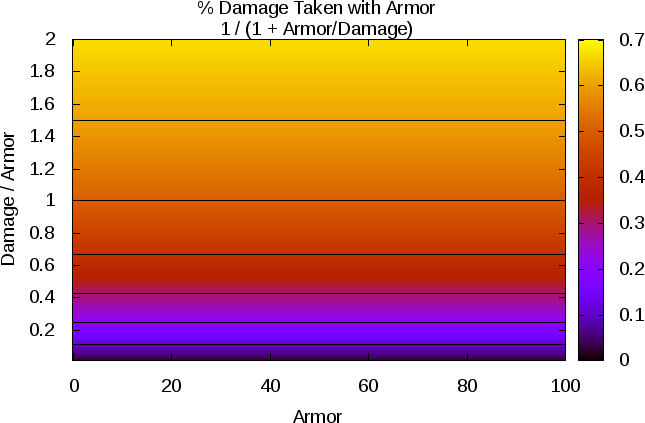
: EtMarc1-relative.png (21.03 KiB) Viewed 6303 times

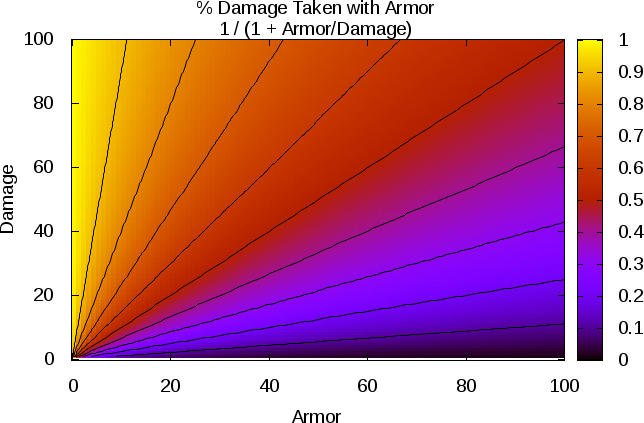
: EtMarc1.png (44.37 KiB) Viewed 6303 times

As you can see, your method is very similar to the previous method used in ToME.

Anyway, to quote yufra regarding my method:

yufra wrote:The formula is complicated to explain, but I think the behavior will be quite intuitive. Basically we just tell people that high armor will completely block low amounts of damage [...], and that as damage increases the effective reduction decreases.

ToME: the Tales of Maj'Eyal

How should "Armor" work?

How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?

Re: How should "Armor" work?